Since the terms involving n cancel out, this can be viewed as either the population covariance and variance or the sample covariance and variance.
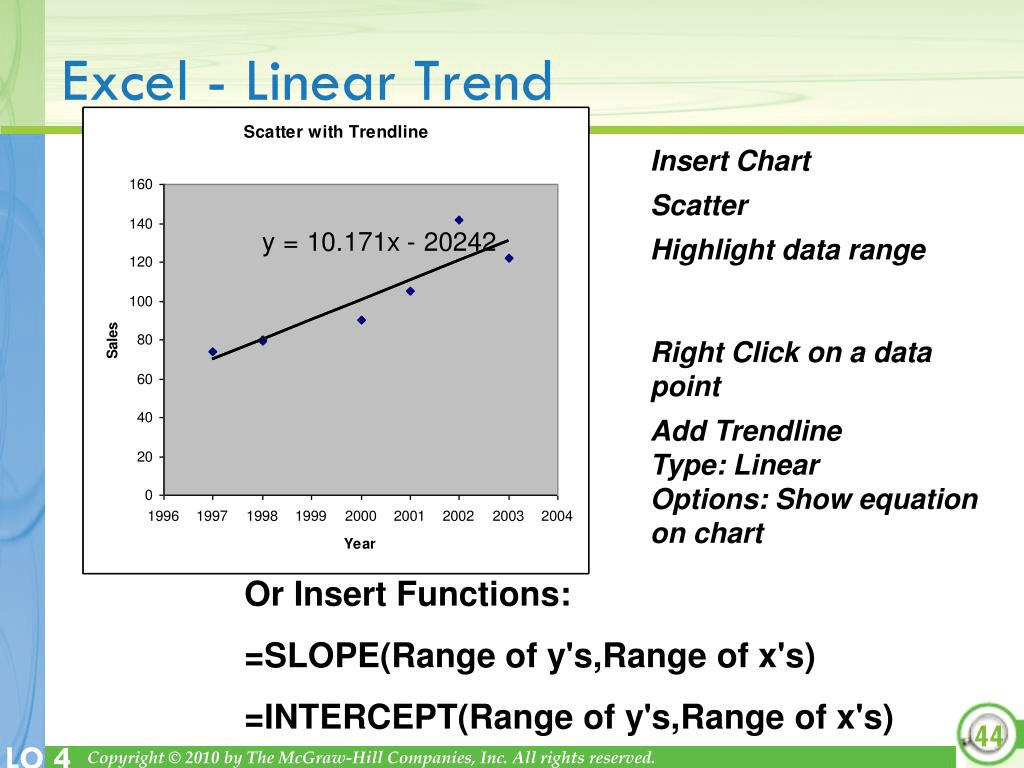
Observation: The theorem shows that the regression line passes through the point ( x̄, ȳ) and has the equation Two proofs are given, one of which does not use calculus.ĭefinition 1: The best fit line is called the regression line.
Theorem 1: The best fit line for the points ( x 1, y 1), …, ( x n, y n) is given byĬlick here for the proof of Theorem 1. A mathematically useful approach is therefore to find the line with the property that the sum of the following squares is minimum. The best fit line is the line for which the sum of the distances between each of the n data points and the line is as small as possible. the value of y where the line intersects with the y-axisįor our purposes, we write the equation of the best fit line asįor each i, we define ŷ i as the y-value of x i on this line, and so Recall that the equation for a straight line is y = bx + a, whereĪ = y-intercept, i.e. We now look at the line in the xy plane that best fits the data ( x 1, y 1), …, ( x n, y n).
In Correlation we study the linear correlation between two random variables x and y.